PDF

Geometriakulma: Käyrän pituus

Edellisen geometriakulman mukaan luontevin tapa tasokäyrän esittämiseen on parametriesitys: käyrän pisteiden koordinaatit esitetään käyräparametrin t funktioina x(t), y(t), jolloin jokaista parametriarvoa t (joltakin tarkasteluväliltä) vastaa käyrän piste (x(t),y(t)). Jos kyseessä on avaruuskäyrä, tarvitaan kolmatta koordinaattia varten kolmas funktio z(t).

Tasokäyrä voidaan esittää vektorimuodossa $\vec{r}(t) = x(t)\,\vec{i} + y(t)\,\vec{j}$, avaruuuskäyrä vastaavasti $\vec{r}(t) = x(t)\,\vec{i} + y(t)\,\vec{j} + z(t)\,\vec{k}$. Tässä $\vec{r}(t)$ on käyrän pisteen paikkavektori, so. origosta parametriarvoa t vastaavaan käyrän pisteeseen osoittava vektori.

Olkoon siis tarkastelun kohteena taso- tai avaruuskäyrä $\vec{r}(t)$, $t \in [a,b]$.

Käyrän pituutta voidaan approksimoida valitsemalla käyrältä järjestyksessä pisteet P₀, P₁, $\dots$, P_n, missä P₀ on käyrän alkupiste ja P_n loppupiste, ja yhdistämällä nämä murtoviivalla. Mitä enemmän pisteitä valitaan ja mitä tiheämmin ne sijaitsevat, sitä tarkemmin murtoviivan pituus tuntuisi - ainakin riittävän säännöllisellä käyrällä - vastaavan käyrän pituutta. Käyrän pituus voitaisiin siten suoranaisesti määritellä murtoviivan pituuden raja-arvoksi, kun jakoa tihennetään.

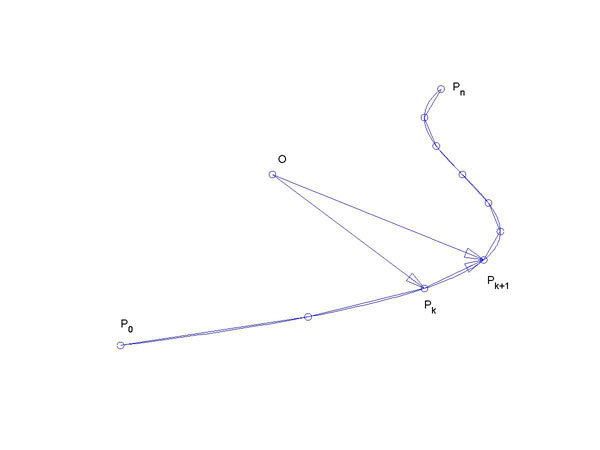
Pisteitä P_k ja P_k+1 yhdistävän janan pituus saadaan vastaavien paikkavektoreiden erotusvektorin pituutena:

$$\vert\Delta \vec{r}_k\vert = \vert\vec{r}(t_{k+1}) - \vec{r}(... ...2 + \left(\frac{\Delta y_k}{\Delta t_k}\right)^2}\,\Delta t_k.$$

Avaruuskäyrän tapauksessa on luonnollisesti lisättävä z-koordinaatista johtuvat termit. Murtoviivan pituus on osajanojen pituuksien summa:

$$\sum_{k=0}^{n-1} \vert\Delta \vec{r}_k\vert = \sum_{k=0}^{n-1... ...2 + \left(\frac{\Delta y_k}{\Delta t_k}\right)^2}\,\Delta t_k.$$

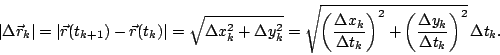
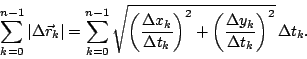
Kun jakopisteiden määrää lisätään ja jakoa samalla tihennetään, kasvaa summan termien määrä ja samalla jokainen termi $\vert\Delta \vec{r}_k\vert$ lähestyy nollaa. Ei siis ole selvää, miten raja-arvon käy. Määrätty integraali on juuri tämäntyyppisen summan raja-arvo. Se pitäisikin mieluummin mieltää summan raja-arvoksi kuin pinta-alaksi.

Koska juurilausekkeen raja-arvo on

$$\lim_{t_{k+1} \rightarrow t_k} \sqrt{\left(\frac{\Delta x_k}{... ... = \sqrt{x'(t_k)^2 + y'(t_k)^2} = \vert{\vec{r}\,}'(t_k)\vert,$$

saadaan summalausekkeen raja-arvoksi integraali

$$\int_a^b \vert{\vec{r}\,}'(t)\vert\,dt.$$

Tämä antaa siis käyrän pituuden. Vektorin derivointi tapahtuu yksinkertaisesti komponenteittain: ${\vec{r}\,}'(t) = x'(t)\,\vec{i} + y'(t)\,\vec{j}$.

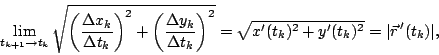
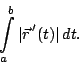
Edellä oleva raja-arvopäättely on hieman ylimalkainen. Oikean idean se kuitenkin antaa.

Esimerkkinä olkoon ellipsi x²/a² + y²/b² = 1, missä a > b. Tämän parametriesityksen $x(t) = a\cos t$, $y(t) = b\sin t$, $0 \le t \le 2\pi$, perusteella saadaan kehänpituudelle integraali

$$\int_0^{2\pi} \sqrt{a^2 \sin^2 t + b^2 \cos^2 t}\,dt.$$

Tämän integrointi ei onnistu alkeisfunktioiden avulla. Se on palautettavissa erääksi erikoisfunktioksi, jota kutsutaan elliptiseksi integraaliksi. Symbolinen laskentaohjelma Mathematica tuntee tämän nimellä $\text{EllipticE}$.

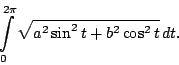
Kehänpituudelle saadaan tällöin lauseke $4a\text{EllipticE}(1 - b^2/a^2)$, mikä on laskettavissa Mathematican versiolla 2.2. Uudemmat versiot sen sijaan tuntuvat antavan väärän tuloksen... Mathematican pahin kilpailija Maplekään ei selviä täysin kunnialla ennen kuin versiossa 6.

Ruuviviiva on avaruuskäyrä, jonka yhden kierroksen parametriesitys on $x(t) = a\cos t$, $y(t) = a \sin t$, z(t) = bt, $0 \le t \le 2\pi$. Edellä johdettu integraali antaa helposti tämän pituudeksi $2\pi\sqrt{a^2+b^2}$.

Sama tulos on myös saatavissa alkeellisella geometrialla: Jos lieriöpinta, jolla ruuviviiva sijaitsee, leikataan jotakin sivuviivaa pitkin auki ja taivutetaan tasoksi, tulee yhtä kierrosta vastaavasta ruuviviivasta kalteva jana. Tämän vaakasuoran projektion pituus on lieriön pohjaympyrän kehänpituus eli $2\pi a$; janan pystysuora projektio on z-koordinaatin muutos eli $2\pi b$. Pythagoraan lause antaa tällöin käyrän pituuden!

Kerrottakoon lopuksi edellisessä geometriakulmassa pohdittaviksi annettujen käyrien parametriesitykset:

$$\begin{align*}&x = \cos{3t}, \quad y = \sin{4t}; \\ &x = t^3 - 2t, \quad y = \f... ...5$ }; \\ &x = 1 + \cos t, \quad y = \sin t, \quad z = 2 \sin(t/2). \end{align*}$$

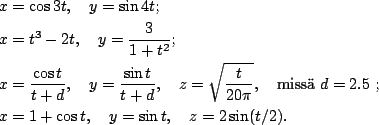
Parametrivälien pohtiminen jääköön edelleen lukijalle.

Periaatteessa samantyyppisiä käyriä voi muodostaa monilla muillakin parametrisoinneilla. Kolmas käyrä on ruuviviivan muunnelma. Neljännessä projektio xy-tasoon on ympyrä ja z-koordinaatti on määrätty siten, että käyrä sijaitsee origokeskisellä pallolla; kyseessä on siten pallon ja lieriön leikkauskäyrä.

Simo K. Kivelä

Solmu 3/1999-2000
2000-03-03