

Solmun tietokonepalstalla tutkitaan, mitä tekemistä matematiikalla ja tietotekniikalla on keskenään. Ensimmäisenä tulee varmaan mieleen tietokoneiden käyttö laskennassa ja visualisoinnissa, siis tietotekniikan soveltaminen matematiikkaan. Alojen syvempää yhteyttä valottaa se, miten matematiikkaa käytetään tietotekniikassa. Sitä esittelee tämä ensimmäinen osa.
Tällä kertaa tutkitaan yhden esimerkin avulla algoritmin käsitettä sekä hieman siihen liittyvää matematiikkaa. Algoritmi on lyhyesti sanottuna "resepti", jonka avulla tietokone osaa suorittaa jonkin tehtävän, esimerkiksi järjestää joukon lukuja tai valita tekstikappaleen rivinvaihdot niin, että tulos on jonkin kriteerin mielessä optimaalinen. Algoritmin toteuttaa yleensä tietokoneohjelma tai ohjelman osa, mutta ei millainen tahansa: vaadimme, että ohjelma pysähtyy ja antaa oikean tuloksen. (Tämän määritelmän mukaan esimerkiksi ydinvoimalan valvontaohjelma ei välttämättä toteuta mitään algoritmia, sillä sen ei kuulu pysähtyä eikä tuottaa mitään lopputulosta vaan vastata ärsykkeisiin järkevällä tavalla. Kuitenkin se luultavasti sisältää algoritmeja: esimerkiksi yksi sen aliohjelma saattaisi tutkia, antavatko reaktorista saadut mittaukset aihetta hälytykseen.)
Tämän artikkelin ymmärtämiseksi lukijan täytyy tuntea ohjelmoinnin alkeet ja jokin lausekieli, esimerkiksi Ada, Java (Java on Sunin rekisteröity tavaramerkki) tai C. Emme tässä kirjoita algoritmeja millään tällaisella kielellä, vaan esitämme ne eräänlaisella pseudokielellä, jollaista jokainen perusteet tunteva osaa toivottavasti lukea. Merkinnöistä on syytä huomata, että ilmaisemme lohkorakenteen pelkästään sisennyksellä (Pythonin tapaan) ja sijoituksen symbolilla :=
Saman tehtävän voi yleensä ratkaista usealla erilaisella algoritmilla, mutta mikä tahansa algoritmi ei sovi käytännön ratkaisuksi. Hyvä algoritmi ei tuhlaa aikaa eikä tilaa.
Tärkein algoritmin aikavaatimukseen vaikuttava seikka on tietysti syöte, joka tiivistetään nopeustarkasteluissa yleensä yhteen lukuun. Tavallisesti tarkastellaan syötteen kokoa, mutta joskus jokin muu sen monimutkaisuuden tunnusluku voi olla olennaisempi. Suoritusaika riippuu tietysti myös käytetystä tietokoneesta, ohjelmointikielestä, muista ajossa olevista ohjelmista ja niin edelleen. Koska tällaiset tekijät vaikeuttaisivat analyysiä tarpeettomasti, ne "abstrahoidaan pois" tekemällä yksinkertaistavia oletuksia.
Tärkein oletus on, että algoritmi suoritetaan peräkkäisten alkeisoperaatioiden sarjana, ja että jokainen alkeisoperaatio vie vakioajan. Kertolasku voi olla kymmenen kertaa hitaampi kuin yhteenlasku, mutta tästä ei välitetä - tärkeää on, että alkeisoperaatioiden aikavaatimukselle on jokin yläraja.
Edelleen unohdetaan jopa alkeisoperaatioiden tarkka lukumäärä ja
lasketaan asymptoottinen aikavaatimus.
Jos syötteen koolla n tarvitaan 3n2+5n-1 alkeisoperaatiota,
sanotaan vain, että aikavaatimus on luokkaa n2, sillä
molemmat n:n funktiot kasvavat suunnilleen yhtä nopeasti.
Kirjoitamme tämän kaavana 3n2+5n-1= (n2).
(n2).
Matemaatikon täytyy tietysti määritellä, mitä "suunnilleen yhtä
nopeasti" tarkoittaa. Kun g on funktio luonnollisilta
luvuilta ei-negatiivisille reaaliluvuille, merkitsemme  (g(n)):llä niiden
funktioiden f luokkaa, jotka eroavat g:stä
vain vakiokertoimella:
(g(n)):llä niiden
funktioiden f luokkaa, jotka eroavat g:stä
vain vakiokertoimella:

 (f(n)) kuten yllä.
Merkinnän etu nähdään, kun f:n paikalla on konkreettinen funktio:
voidaan puhua vaikkapa luokasta
(f(n)) kuten yllä.
Merkinnän etu nähdään, kun f:n paikalla on konkreettinen funktio:
voidaan puhua vaikkapa luokasta  (2n) ilman monimutkaisia
kiertoteitä.)
(2n) ilman monimutkaisia
kiertoteitä.)
Silloin kun  -merkintä esiintyy yhtälön oikealla
puolella, sovitaan että =-merkki tarkoittaakin
merkkiä
-merkintä esiintyy yhtälön oikealla
puolella, sovitaan että =-merkki tarkoittaakin
merkkiä 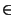 .
Siis f(n)=
.
Siis f(n)= (g(n)) tarkoittaa, että f(n) voidaan
"puristaa" c1g(n):n ja c2g(n):n väliin, kunhan n:n annetaan
kasvaa tarpeeksi suureksi. Voidaan myös ajatella, että
(g(n)) tarkoittaa, että f(n) voidaan
"puristaa" c1g(n):n ja c2g(n):n väliin, kunhan n:n annetaan
kasvaa tarpeeksi suureksi. Voidaan myös ajatella, että  (g(n))
tarkoittaa jotain edellä määritellyn joukon funktiota, jota ei vain
nimetä tarkkaan.
(g(n))
tarkoittaa jotain edellä määritellyn joukon funktiota, jota ei vain
nimetä tarkkaan.
 :n määritelmä sisältää kaksi epäyhtälöä.
Jos jommastakummasta luovutaan, merkitään O tai
:n määritelmä sisältää kaksi epäyhtälöä.
Jos jommastakummasta luovutaan, merkitään O tai 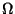 :
:
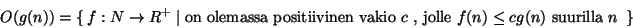
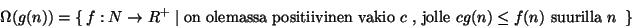
 :aa.
Siinä missä
:aa.
Siinä missä  vastaa suunnilleen
merkkiä
vastaa suunnilleen
merkkiä 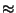 .
O on
.
O on 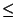 ja
ja 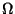 on
on 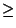 .
.
Algoritmin tilavaatimus tarkoittaa sen tarvitsemien tietokoneen muistipaikkojen lukumäärää. Sitä voidaan myös tutkia asymptoottisesti, mutta se on monesti kiinnostava tarkemminkin - muistin käyttäminen on tyypillisesti melko hidasta, varsinkin jos tilaa kuluu niin paljon että joudutaan turvautumaan levymuistiin.
 (n),
(n),
 (100n2+10000n),
(100n2+10000n),
 (1) ja
(1) ja
 (log1998(n)).
(log1998(n)).
 :n "sisään" kirjoitettava funktio pyritään valitsemaan
mahdollisimman yksinkertaiseksi, ja esimerkiksi logaritmin kantalukua
ei merkitä.
:n "sisään" kirjoitettava funktio pyritään valitsemaan
mahdollisimman yksinkertaiseksi, ja esimerkiksi logaritmin kantalukua
ei merkitä.
 (f(n)),
(f(n)),
 (g(n)) jos ja vain jos g(n) =
(g(n)) jos ja vain jos g(n) =  (f(n)) ja
(f(n)) ja
 (g(n)), g(n) =
(g(n)), g(n) =  (h(n)), niin f(n) =
(h(n)), niin f(n) =  (h(n))
(h(n))
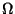 (f(n)).
(f(n)).
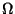 (g(n)).
(g(n)).
Tässä artikkelissa tutkitaan esimerkkinä muutamaa algoritmia, joilla lasketaan Fibonaccin lukuja. Ongelma on yksinkertainen: on annettu luku n, ja on laskettava F(n), missä F(n) määritellään palautuskaavalla
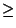 0,
0,
Algoritmien aikavaatimuksia on luonnollista tarkastella n:n funktioina.
Ensimmäinen algoritmimme naiivi-fibonacci perustuu suoraan määritelmään: jos n on 0 tai 1, palautetaan määritelmästä saatava arvo, muuten lasketaan rekursiivisesti F(n-1) ja F(n-2) ja summataan tulokset.
On tärkeää varmistua, että algoritmin suoritus päättyy. Tämä nähdään
induktiolla: Jos n 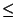 1, asia on selvä. Muussa tapauksessa nojataan
siihen, että suoritus päättyy parametrin arvoilla n-2 ja n-1.
1, asia on selvä. Muussa tapauksessa nojataan
siihen, että suoritus päättyy parametrin arvoilla n-2 ja n-1.
Tämä algoritmi on siinä mielessä elegantti, että se muistuttaa Fibonaccin lukujen määritelmää. Se kuvaa, mitä lasketaan, eikä siitä edes näe aivan helposti, miten laskenta tapahtuu. Kuten kohta huomaamme, algoritmi on toivottoman hidas - tämä on liian korkean tason ohjelmointia tavalliselle lausekielelle. (On ohjelmointikieliä, esimerkiksi Prolog, joilla ohjelmoidaan juuri tällä tavalla.)
Merkitään algoritmin aikavaatimusta T(n):llä. Jos n 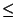 1,
T(n) on vakio; muuten
T(n) = T(n-2)+T(n-1)+vakio.
Ilmeisesti T(n)=
1,
T(n) on vakio; muuten
T(n) = T(n-2)+T(n-1)+vakio.
Ilmeisesti T(n)=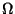 (F(n)).
Myöhemmin nähdään, että F(n)=
(F(n)).
Myöhemmin nähdään, että F(n)= (
(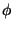 n),
missä
n),
missä 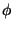 > 1, joten
tämän algoritmin aikavaatimus on vähintään eksponentiaalinen!
(Itse asiassa T(n)=
> 1, joten
tämän algoritmin aikavaatimus on vähintään eksponentiaalinen!
(Itse asiassa T(n)= (F(n)), mutta toisen suunnan todistaminen
on hieman työläämpää, eikä se ole kovin kiinnostavaa - jos
aikavaatimus on eksponentiaalinen, algoritmi on käytännössä aivan
liian hidas.)
(F(n)), mutta toisen suunnan todistaminen
on hieman työläämpää, eikä se ole kovin kiinnostavaa - jos
aikavaatimus on eksponentiaalinen, algoritmi on käytännössä aivan
liian hidas.)
Rekursiivisen algoritmin vika on, että se "unohtaa" tietoa. Kokeilepa laskea vaikka F(10): todennäköisesti kirjoitat paperille peräkkäisiä Fibonaccin lukuja, niin että et joudu laskemaan samoja lukuja uudestaan. Itse asiassa riittää muistaa kaksi edellistä lukua: aloitetaan F(0):sta ja F(1):stä, lasketaan F(2), sitten F(1):n ja F(2):n avulla F(3) jne.
Olkoon aluksi a=F(0)=0 ja b=F(1)=1. Silmukan k:nnen kierroksen jälkeen haluamme muuttujien arvoiksi a=F(k) ja b=F(k+1). Muuttujan a uusi arvo on suoraan b:n vanha arvo, ja b:n uusi arvo on a:n ja b:n vanhojen arvojen summa.
Alkutoimenpiteisiin kuluu vakion verran aikaa, samoin silmukan yhdellä kierroksella. Kierroksia on n-1, joten algoritmin aikavaatimus on
 (n).
(n).
Nyt pääsemme lopulta käyttämään apuna matematiikkaa. Seuraavan algoritmin ymmärtäminen vaatii lineaarialgebran perustietoja sen verran, että matriisien kertolasku on tuttu asia.
Edellisessä algoritmissa on kaksi muuttujaa, joita päivitetään joka kierroksella. Jos muuttujat ajatellaan 2-vektorin alkioiksi, päivitys on lineaarimuunnos: jos ohjelmointikielessämme voisi käyttää matriisioperaatioita, päivityksen voisi kirjoittaa sijoituksena
![[a; b] := M [a; b], missä M = [0 1; 1 1]](M-sijoitus.gif) .
.
![[F(k+1); F(k+2)] = M [F(k); F(k+1)]](M-saanto.gif)
![[F(n-1); F(n)] = M^(n-1) [F(0); F(1)]](M-yleistys.gif) .
.
Jos matriisin M voisi korottaa potenssiin n-1 nopeammin kuin kertomalla se itsellään n-2 kertaa, olisi ongelmaamme löydetty nopeampi ratkaisu. Tietysti matriisit pitää esittää jonakin tietorakenteena, ja niiden kertolasku pitää toteuttaa, mutta tämä on 2*2-matriisien tapauksessa helppoa, emmekä keskity tähän seikkaan enempää vaan käytämme pseudokielessämme vapaasti matriisimuuttujia. (Suurten matriisien esittäminen ja kertolasku ei sen sijaan ole triviaalia.) Merkitsemme matriisien kertolaskua tavalliseen tapaan kirjoittamalla kerrottavat vierekkäin.
Tässä aliluvussa yritämme löytää nopean tavan laskea matriisien
potensseja. Tavoite on laskea Mn-1, mutta koska
potenssilaskualgoritmi voi olla hyödyllinen muutenkin, muotoilemme
tehtävän siistimmin: on laskettava Ak, missä A on matriisi
ja k 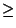 0 kokonaisluku.
0 kokonaisluku.
Voisiko matriisipotenssin laskea nopeammin kuin k-1 kertolaskulla? Kokeile: Laske M2, M4 ja M8. Montako matriisikertolaskua tarvitsit? Entä montako tavallisten lukujen kertolaskua tarvitset laskiessasi lukua 78?
Seuraavassa esityksessä ei oikeastaan ole mitään merkitystä sillä, että potenssiin korotettavat oliot ovat matriiseita - algoritmi toimii myös luvuille. (Oikeastaan tarkastelu pätee minkä tahansa ryhmän alkioille - olennaista on kertolaskun assosiatiivisuus, s.o. laki (AB)C=A(BC). Ilman tätä ominaisuutta potenssimerkintäkään ei ole järkevä.)
Luultavasti huomasit, että M8:n laskemiseen tarvitaan vain kolme kertolaskua:
![M^8 = [1 1; 1 2]^4 = [2 3; 3 5]^2 = [13 21; 21 34]](M8.gif)
Yritetään induktiivista lähestymistapaa: Kuvitellaan, että Aj osataan laskea, kun j<k, ja mietitään Ak:n laskemista. Jos k on parillinen, voidaan soveltaa edellisen kappaleen ideaa: lasketaan Ak/2 ja kerrotaan se itsellään. Jos taas k on pariton, niin varmasti k-1 on parillinen, ja Ak = A Ak-1. Saadaan algoritmi rekursiivinen-potenssi.
Aikavaatimuksen laskemiseksi kirjoitetaan k binäärilukuna. Jokaisella kerralla aliohjelman kutsuessa itseään k:n binääriesityksen lopusta joko katoaa nolla (jos k on parillinen, se jaetaan kahdella) tai muuttuu ykkönen nollaksi (jos k on pariton, siitä vähennetään 1). Kutsuja on siis yhteensä
 (log k).
(log k).
Algoritmin tilavaatimus on
myös  (log k) rekursiivisten kutsujen
takia. Tilan kulutus on "piilossa", mutta jokainen rekursiivinen kutsu
jättää muistiin tiedon siitä, mitkä ovat muuttujien arvot kutsuvassa
aliohjelmassa. Tässä tapauksessa rekursio voidaan muuntaa silmukaksi,
joka tekee aivan samat laskutoimitukset mutta aloittaa suoraan pienimmistä
A:n potensseista ja kokoaa niistä Ak:n. Ei ole aivan ilmiselvää,
miten tämä tehdään, ja ohjelmoinnin harrastajan kannattaakin jäädä
miettimään asiaa hetkeksi ennen kuin jatkaa lukemista.
(log k) rekursiivisten kutsujen
takia. Tilan kulutus on "piilossa", mutta jokainen rekursiivinen kutsu
jättää muistiin tiedon siitä, mitkä ovat muuttujien arvot kutsuvassa
aliohjelmassa. Tässä tapauksessa rekursio voidaan muuntaa silmukaksi,
joka tekee aivan samat laskutoimitukset mutta aloittaa suoraan pienimmistä
A:n potensseista ja kokoaa niistä Ak:n. Ei ole aivan ilmiselvää,
miten tämä tehdään, ja ohjelmoinnin harrastajan kannattaakin jäädä
miettimään asiaa hetkeksi ennen kuin jatkaa lukemista.
Seuraavassa ratkaisussa käytämme apuna invariantin käsitettä. Nimensä mukaisesti invariantti on jokin muuttumaton asia - tässä tarkoitamme sillä erästä lauseketta, jonka arvo on sama ennen silmukan kutakin "kierrosta" ja sen jälkeen. Käytämme apumuuttujaa X, jonka arvona on aluksi identiteettimatriisi, ja pyrimme säilyttämään invarianttina lausekkeen X Ak. Tavoitteemme on muuttaa jokaisella kierroksella X:n, A:n ja k:n arvoa niin, että k:n arvo pienenee aina ja invariantti pysyy samana. Lopulta k=0, ja silloin X on haluttu vastaus. Jos merkitsemme Ai:llä, Xi:llä ja ki:llä muuttujien arvoja silmukan i:nnen kierroksen lopussa, invarianssiehdosta seuraa yhtäsuuruuksien ketju
Lähdetään siis muodostamaan algoritmia. Jotta se toimii samalla tavalla kuin rekursiivinen-potenssi, valitsemme silmukan kierroksella suoritettavat operaatiot k:n parillisuuden mukaan, ja joko jaamme k:n kahdella tai vähennämme siitä ykkösen. Jos k on parillinen, invarianssiehto voidaan nyt kirjoittaa muotoon
Siinä olikin jo kaikki! Kun invariantti oli valittu hyvin, algoritmia kirjoittaessa meille ei jäänyt juurikaan vaihtoehtoja. Ensi katsomalta iteratiivinen-potenssi voi olla vaikea ymmärtää; avain on invariantti X Ak.
![A := [x y; z w]](xyzw.gif)
![M = [0 1; 1 1]](0111.gif)
![[p q; q p+q]](pqqp+q.gif)
Vielä nopeamman algoritmin löytämiseksi jatkamme Fibonaccin lukujonon ominaisuuksen tutkimista. Jonon määrittelevät differenssiyhtälö
Tehdään nyt rohkea arvaus, että Fibonaccin luvut saadaan jonkin luvun r potensseina: F(n)=rn. Jos näin on, r:lle saadaan differenssiyhtälöstä ehto
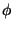 = (1 +
= (1 + 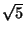 )/2 ja
)/2 ja
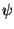 = (1 -
= (1 - 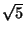 )/2. Valitettavasti kumpikaan näistä ei tuota
Fibonaccin lukuja, joten arvauksemme oli väärä.
)/2. Valitettavasti kumpikaan näistä ei tuota
Fibonaccin lukuja, joten arvauksemme oli väärä.
Olemme silti havainneet tärkeän asian: n:n funktiot 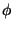 n ja
n ja
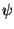 n toteuttavat differenssiyhtälön. Nyt voimme
nimittäin konstruoida niiden avulla lisää ratkaisuja. Ensinnäkin,
jos G(n) on differenssiyhtälön ratkaisu, niin on myös C G(n)
jokaisella vakiolla C. Toiseksi kahden ratkaisun summa on myös
ratkaisu. Nämä tiedot yhdistämällä saamme parametroidun ratkaisun
n toteuttavat differenssiyhtälön. Nyt voimme
nimittäin konstruoida niiden avulla lisää ratkaisuja. Ensinnäkin,
jos G(n) on differenssiyhtälön ratkaisu, niin on myös C G(n)
jokaisella vakiolla C. Toiseksi kahden ratkaisun summa on myös
ratkaisu. Nämä tiedot yhdistämällä saamme parametroidun ratkaisun
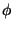 n + C2
n + C2 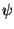 n.
n.
Jos nyt saadaan määrättyä sellaiset vakiot C1 ja C2, että alkuehdot F(0)=0, F(1)=1 toteutuvat, on löydetty lauseke F(n):lle. Saadaan yhtälöpari
| C1 + C2 | = | 0, |
C1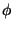 + C2 + C2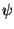 |
= | 1, |
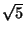 ,
C2 = -1/
,
C2 = -1/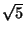 .
.
Koska
|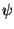 |<1, toisen termin vaikutus johtamassamme
lausekkeessa pienenee nopeasti n:n kasvaessa.
Kun n
|<1, toisen termin vaikutus johtamassamme
lausekkeessa pienenee nopeasti n:n kasvaessa.
Kun n 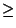 0,
0,
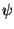 n| < 1/2,
n| < 1/2,
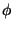 n ja pyöristää se lähimpään kokonaislukuun.
n ja pyöristää se lähimpään kokonaislukuun.
Nyt olemme siis löytäneet hyvin yksinkertaisen algoritmin
potenssilasku-fibonacci,
joka toimii vakioajassa kaikilla n; sen aikavaatimus on
siis  (1).
(1).
Tällä algoritmilla on kuitenkin se rajoitus, että sen suorittamiseksi täytyy laskea reaaliluvuilla. Useimmat ohjelmointikielet ja tietokoneet tukevat ns. liukulukuja, joilla voi tehdä reaalilukujen laskutoimituksia likimääräisesti. Algoritmimme voi hyödyntää liukulukulaskentaa melko hyvin, koska siinä joka tapauksessa tehdään lopuksi pyöristys: voimme toivoa, että laskennassa tapahtuvat virheet ovat niin pieniä, että ne eivät vaikuta lopputulokseen. Tällaisia asioita ei ole kuitenkaan aivan helppo todistaa.
Etsi sekä yleiset ratkaisut että ratkaisut alkuehdoilla f(0)=1, f'(0)=2.
Etsi sekä yleiset ratkaisut että ratkaisut alkuehdoilla F(0)=1, F(1)=2.
Olemme nähneet, että tietokoneohjelmaa voi nopeuttaa paljon suunnittelemalla sen hyvin. Aina ei tietenkään saavuteta näin dramaattista tulosta: aikavaatimus parani toivottomasta eksponentiaalisesta varsin hyvään logaritmiseen, tai eräillä ehdoilla vakioksi. Toivottavasti lukija on huomannut, että matematiikka ei ole tietojenkäsittelijälle lainkaan turha tieteenala.
Jouni Seppänen
Jouni.Seppanen@iki.fi