Matematiikka on yleismaailmallista kaavojen kieltä. Kuitenkin matematiikasta puhutaan ja kirjoitetaan sanoja käyttäen niin kuin muistakin asioista. Kun matematiikan käsitteet ovat usein vaikeita omaksua, saattaisi olla hyödyksi ja huviksi pohdiskella niistä käytettävien nimitysten alkuperää tai suomenkielistä merkitystä ja sanojen ja nimitysten joskus yllättäviäkin kytkentöjä. Aika monet matematiikan sanat ovat vierasperäisiä. Monesti sama sana esiintyy hiukan muuntuneena lähes kaikissa Euroopan kielissä. Tämä tietysti helpottaa tiedonvälitystä ja perustelee sen, että kaikkia sanoja ei ole käännetty aidosti suomenkielisiksi.
Itse matematiikka-sana on peräisin antiikin Kreikasta, ilmeisesti jo n. 500 eKr. vaikuttaneilta pythagoralaisilta. Mathesis tarkoitti alkuaan 'oppia' tai 'asioita, jotka on opittava'. Erityisesti matematiikan erotti eräistä muista sivistyksen aloista kuten kirjallisuudesta se, että matematiikkaa ymmärsi ja arvosti vain henkilö, joka oli sitä erityisesti opiskellut. Matematiikan tärkeys kaiken muun opin rinnalla näkyy nykykielen sanassa triviaali 'tavallinen, yksinkertainen, helppo'. Tämän latinapohjaisen sanan ytimenä on trivium 'kolme tietä'. Se tarkoitti vanhan, jo Aristoteleen esittämän opin ja koulutuksen seitsenjaon alkeellisempaa "humanistista" osuutta eli grammatiikka, retoriikkaa ja dialektiikkaa. Loput neljä ainetta muodostivat quadriviumin eli 'neljä tietä'. Nämä epätriviaalit asiat olivat sitten aritmetiikka, geometria, astronomia ja musiikki (joka miellettiin matemaattiseksi opiksi).
Myös matematiikan kaksi tärkeää osa-aluetta - geometria ja aritmetiikka ovat saaneet nimensä kreikasta. Geometria tarkoittaa alun perin maan mittausta (ja siis samaa kuin nykykielen geodesia, joka on suomennettuna maan jakamista). Aritmetiikka tulee kreikan sanasta arithmos, joka tarkoittaa lukua. Antiikin Kreikassa aritmetiikalla ymmärrettiin oppia lukujen teoreettisista ominaisuuksista, kuten esim. jaollisuudesta. Arkipäivän laskentoa, sitä mistä matematiikan oppiminen tavallisesti aloitetaan, kutsuttiin logistiikaksi.
Sana algebra ei ole alkuaan kreikasta. Ensitavu al- osoittaa sanan arabialaisperäiseksi. Algebra on lähtöisin 800-luvulla eläneen arabimatemaatikon al-Khowarizmin teoksesta Al jabr w'al muqabalah. Teos käsitteli yhtälöiden ratkaisemista, ja sen nimessä esiintyvät arabian sanat tarkoittavat operaatioita, joilla yhtälöitä sievennetään siirtämällä termejä puolelta toiselle ja yhdistelemällä samanmuotoisia termejä. Jabr merkitsee katkenneiden palojen yhdistämistä. Cervantesin Don Quijotessa tavataan algebristi, katkenneiden luiden lastoittaja. Al-Khowarizmin nimi elää myös tärkeässä matematiikan ja tietojenkäsittelyn termissä algoritmissa. Al-Khowarizmi kannatti laskentoa Intiassa kehittyneen kymmenjärjestelmän numeroilla (esim. roomalaisten numeroiden sijasta), ja hänen aiheesta kirjoittamansa kirja oli keskeinen tämän aikanaan vallankumouksellisen merkintätavan puolestapuhuja. Kymmenjärjestelmän myötä käyttöön tulleita uusia laskutapoja ruvettiin kutsumaan Al-Khowarizmin mukaan algorismiksi; aikojen kuluessa sana sai nykyisen muotonsa ja merkityksensä.
Palataan laskentoon eli aritmetiikkaan. Summa on alun perin latinan summus eli supremus eli 'ylin, korkein'. Yhteenlaskun tulos oli vanhaan aikaan tapana kirjoittaa yhteenlaskettavien yläpuolelle, ja onhan positiivisten lukujen summa yhteenlaskutehtävässä esiintyvistä luvuista suurin. Kun yhteenlasku lausutaan sanaa plus käyttäen, puhutaan myös latinaa. Plus tarkoittaa yksinkertaisesti 'enemmän'. Vastaavasti miinus on latinan minus, jonka merkitys on 'vähempi, pienempi'. Ministeri on herraansa vähäisempi palvelija. Samaa lähtöä on tietysti minimi. (Maksimi tulee latinan magnus 'suuri'-sanan superlatiivimuodosta. Samaan sanaan palautuva komparatiivi magis 'enemmän' on pohjana usean matematiikanopettajankin tittelinä olevalle magisterille eli maisterille.)
Ennen kuin nykyiset +- ja --merkit vakiintuivat käyttöön
(1500--1600-luvuilla), yhteen- ja vähennyslaskuja oli tapana merkitä
kirjaimin p ja m; näiden päälle merkittiin usein viiva kertomaan
kirjainten erityismerkityksestä. Arvellaan, että vähennyslaskun - on
syntynyt siitä, että m alkoi unohtua
merkinnästä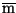 
.
- Neliöjuuren
merkki 
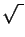on muuten kehkeytynyt
kirjaimesta r, joka taas on latinan juurta tarkoittavan sanan radix
ensimmäinen kirjain. Radix löytyy vaikkapa sanasta retiisi;
neliö- ja punajuurten yhdistäminen ei ole ihan niin
hölmöä, kuin miltä se ensin kuulostaa.
Geometrian osa-alue on trigonometria. Sana tulee kreikan kolmiota eli kolmikulmaa tarkoittavasta trigon-sanasta. Trigonometriassa keskeisiä ovat trigonometriset funktiot sini, kosini ja tangentti. Sanan sini historia on mielenkiintoinen ja liittyy tiedon siirtymiseen keskiaikana ensin Intiasta islamilaisen kulttuurin piiriin ja sieltä kristityille länsimaille. Pohjana on sanskritin jiva, joka tarkoitti ympyrän jännettä. Keskiajalla intialaisia kirjoituksia käännettiin arabiaksi. Jivalle ei löytynyt sopivaa arabiankielistä vastinetta, joten se lainattiin arabiaan sellaisenaan, muodossa jiba. Arabiaa kirjoitettaessa vain konsonantit merkitään näkyviin. Niinpä matemaattisia tekstejä arabiasta latinaksi kääntänyt keskiaikainen oppinut Robert Chesteriläinen tulkitsi sanan olevan jaib, joka tarkoittaa mm. merenlahtea, latinaksi sinus. Tangentti trigonometrisenä funktiona liittyy luonnollisella tavalla vaikkapa kulman kylkien ympyrän tangentista erottaman osan pituuteen. Sanan pohjana on latinan tangere 'koskettaa'. Teknisissä laitteissa tangentti onkin usein jonkinlainen kosketin. - Käyrät voivat matematiikassa mennä kosketusta pitemmällekin: avaruuskäyrällä voi olla sitä koskettavan tangentin lisäksi esim. oskuloiva taso. Latinan osculum on 'suudelma'. Jos hahmottelet käyrän y2=x4(1-x2), saat esimerkin oskulaatiopisteestä.
Sitten vähän algebran sanoja. Potenssi tulee latinasta ja tarkoittaa voimaa, mahtavuutta. Sana kuvaa hyvin sitä, että luvun kertominen itsellään kasvattaa ehkä rajustikin lukua. (Ykköstä pienemmän luvun kertominen itsellään ei kuitenkaan ole impotenssia.) Eksponentti puolestaan tarkoittaa osoittajaa, esittäjää, potenssin voimakkuuden näyttäjää. Olisikohan helpompi ajatella, että 1000=103 on kymmenen kolmas mahtavuus ja 3 tämän mahtavuuden esittäjä?
Nykyisin analyysiksi kutsutun matematiikan alan sanoista monet ovat nekin latinaa tai kreikkaa. Analyysi tarkoittaa erottelua (niin kuin kemiassa) tai erittelyä. Klassisessa geometriassa piirtämistehtävän analyysi tarkoitti jo tehdyksi ajatellun konstruktion purkamista osiinsa. Matemaattisen analyysin keskeinen käsite on funktio. Sen pohjana on latinan verbi fungere, joka tarkoittaa 'toimia'. Funktio-sanaa käytetään matematiikan ulkopuolella yleismerkityksessä 'tehtävä'. Matemaattisen erityismerkityksen tälle sanalle otti käyttöön 1600-luvun lopulla Leibniz, toinen differentiaali- ja integraalilaskennan keksijöistä. Differentiaali tarkoittaa erotusta, funktion differentiaali kahden lähekkäisen funktionarvon erotusta. Integraali puolestaan merkitsee 'kokonaista', oikeastaan alkuaan 'koskematonta'. Leibniz käytti aluksi integraalilaskennasta nimeä calculus summatorius - summien yleistyksiähän integraalit ovat. Kokonaisen ja erillisen vastakkaisasettelua edustava parin differentiaali - integraali otti käyttöön Leibnizin sveitsiläinen ystävä Jakob Bernoulli. Englannin kieleen differentiaali- ja integraalilaskentaa merkitsemään on sitten tullut sana calculus. Se on samaa alkuperää kuin kalkki. Muinoin laskelmia tehtiin helmitaulun kaltaisella laskulaudalla, abakuksella, jonka päällä siirreltiin pieniä kalkkikiven palasia, calculi. Laskukivien käyttö jäi merkitsemään kaikkea laskentaa ja laskelmointia, kalkylointia, ja sitten erityiseksi laskumetodiksi miellettyä differentiaali- ja integraalilaskentaa.
Integraalin vastinkäsitteen nimitys derivaatta on
oikeastaan aika huono. Se on peräisin 1700-luvun lopun merkittävältä
ranskalismatemaatikolta Lagrangelta, joka kiinnitti erityistä huomiota
derivaattaan funktiona (ja on mm. vastuussa merkinnöistä f'(x),
f''(x) jne.). Derivaatta f' oli Lagrangelle funktioon f
liittyvä
fonction dérivée eli 'johdettu funktio'. Mutta millaisesta
johtamisesta on kyse, ei paljastu nimityksestä. Saksan kielessä
derivaatta on Ableitung eli johdos. Vuosisadan alun
suomalaisista oppikirjoista voi löytää sanan johdos
merkityksessä 'derivaatta'. Derivaatta ei pelkistetyimmillään ole
funktio ollenkaan, vaan vain luku, joka ilmoittaa funktion arvojen
muutosnopeuden argumentin muutokseen nähden.
Merkintään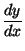 
liittyvä nimitys differentiaaliosamäärä
ilmaisisi täsmällisemmin
asiasisällön, samoin vaikkapa nopeus tai vauhti.
Matti Lehtinen
Matti.Lehtinen@Helsinki.FI