Turistina matematiikassa

Toinen retki. Nuo mainiot binomikertoimet.

C Matkamuistot

Varsinainen retkeily tehtiin Solmussa 1/1997-98. Osa kohteista jäi tuolloin selittämättä. Tätä jälkikatsausta kannattaa seurata edellisen retken matkaopas mukanaan - kohdenumerointikin periytyy sieltä.

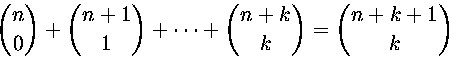
2. Todista oikeiksi yhteenlaskukaavat

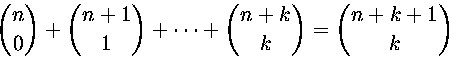
$\begin{displaymath} {n\choose 0}+{n+1\choose 1}+\cdots+{n+k\choose k}={n+k+1\choose k}\end{displaymath}$

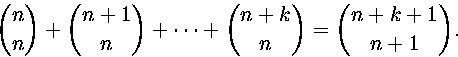
$\begin{displaymath} {n\choose n}+{n+1\choose n}+\cdots+{n+k\choose n}={n+k+1\choose n+1}.\end{displaymath}$

Käytetään induktiota. Kaavoista ensimmäinen on tosi, kun k=0. Jos kaava on tosi arvolla k, pätee

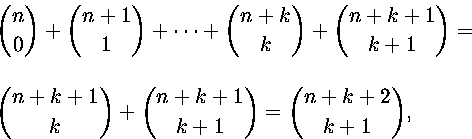
$\begin{displaymath} \begin{split} &{n\choose 0}+{n+1\choose 1}+\cdots+{n+k\choos... ...\choose k}+{n+k+1\choose k+1} = {n+k+2\choose k+1},\end{split}\end{displaymath}$

ja induktioaskel on otettu. Jälkimmäinen kaava seuraa edellisestä, kun otetaan huomioon kaava .

4. Osoita, että $1^2+2^2+\cdots+n^2$ voidaan laskea käyttämällä hyväksi kaavaa (k+1)³-k³=3k²+3k+1. Keksitkö vielä muita tapoja summan laskemiseksi?

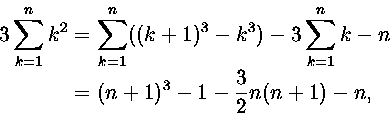
$\begin{displaymath} \begin{split} 3\sum_{k=1}^nk^2&=\sum_{k=1}^n((k+1)^3-k^3)-3\sum_{k=1}^nk- n \\ & = (n+1)^3-1-{3\over 2}n(n+1)-n,\end{split}\end{displaymath}$

joten

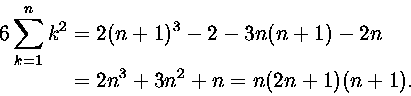
$\begin{displaymath} \begin{split} 6\sum_{k=1}^nk^2 & =2(n+1)^3-2- 3n(n+1)-2n \\ &= 2n^3+3n^2+n=n(2n+1)(n+1).\end{split}\end{displaymath}$

Toinen tapa laskea summa olisi arvata sen olevan muotoa An³+Bn²+Cn+D ja määrittää A, B, C ja D antamalla n:lle neljä eri suurta kokonaislukuarvoa. Saatu kaava voitaisiin sitten todistaa induktiolla paikkansapitäväksi kaikilla n.

5. Laske

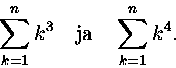
$\begin{displaymath} \sum_{k=1}^nk^3\quad{\rm ja}\quad \sum_{k=1}^nk^4.\end{displaymath}$

Koska

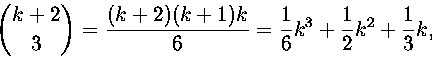
$\begin{displaymath} {k+2\choose 3}={(k+2)(k+1)k\over 6}={1\over 6}k^3+{1\over 2}k^2+{1\over 3}k,\end{displaymath}$

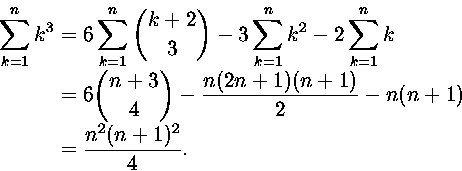
$\begin{displaymath} \begin{split} \sum_{k=1}^nk^3 & = 6\sum_{k=1}^n{k+2\choose... ...+1)(n+1)\over 2}-n(n+1) \\ & = {n^2(n+1)^2\over 4}.\end{split}\end{displaymath}$

Vastaavasti

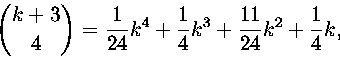
$\begin{displaymath} {k+3\choose 4}={1\over 24}k^4+{1\over 4}k^3+{11\over 24}k^2+{1\over 4}k,\end{displaymath}$

joten

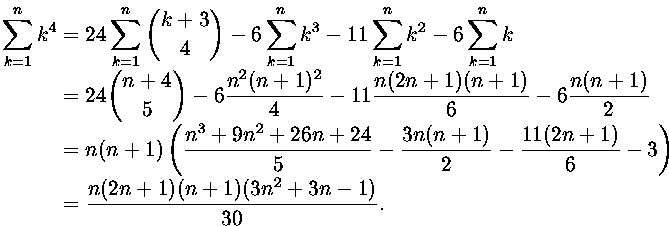
$\begin{displaymath} \begin{split} \sum_{k=1}^nk^4 & = 24\sum_{k=1}^n{k+3\choose... ... 3\right) \\ & = {n(2n+1)(n+1)(3n^2+3n-1)\over 30}.\end{split}\end{displaymath}$

6. Määritä

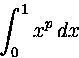
$\begin{displaymath} \int_0^1x^p\,dx\end{displaymath}$

arvoilla p=1, 2, 3, 4, käyttäen hyväksi tietoa

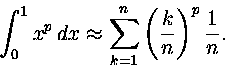
$\begin{displaymath} \int_0^1x^p\,dx\approx \sum_{k=1}^n\left({k\over n}\right)^p{1\over n}.\end{displaymath}$

Integraalia approksimoivien summien arvot ovat

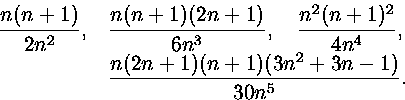
$\begin{displaymath} \begin{split} {n(n+1)\over 2n^2},\quad & {n(n+1)(2n+1)\over ... ...4n^4},\quad\\ &{n(2n+1)(n+1)(3n^2+3n-1)\over 30n^5}.\end{split}\end{displaymath}$

Kun $n\to\infty$ , osamäärät lähestyvät raja-arvoja $\displaystyle{1\over 2}$ , $\displaystyle{1\over 3}$ , $\displaystyle{1\over 4}$ ja $\displaystyle{1\over 5}$ .

9. Johda kaava

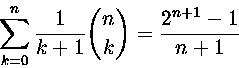
$\begin{displaymath} \sum_{k=0}^n{1\over k+1}{n\choose k}={2^{n+1}-1\over n+1}\end{displaymath}$

integroimalla binomikaava.

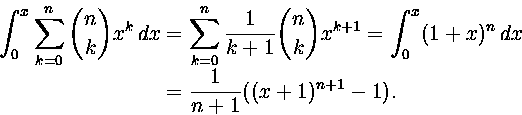
$\begin{displaymath} \begin{split} \int_0^x\sum_{k=0}^n{n\choose k}x^k\,dx &= \su... ...nt_0^x(1+x)^n\,dx \\ &= {1\over n+1}((x+1)^{n+1}-1).\end{split}\end{displaymath}$

Kun tähän sijoitetaan x=1, saadaan heti haluttu kaava.

10. Määritä

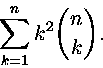
$\begin{displaymath} \sum_{k=1}^nk^2{n\choose k}.\end{displaymath}$

Kohteen 8 jälkimmäisen kaavan perusteella

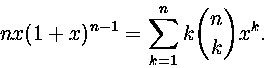
$\begin{displaymath} nx(1+x)^{n- 1}=\sum_{k=1}^nk{n\choose k}x^k.\end{displaymath}$

Kun tämä derivoidaan puolittain, saadaan

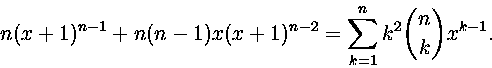
$\begin{displaymath} n(x+1)^{n-1}+n(n-1)x(x+1)^{n-2}=\sum_{k=1}^nk^2{n\choose k}x^{k- 1}.\end{displaymath}$

Kun sijoitetaan x=1, saadaan

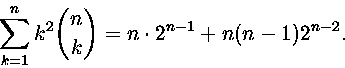
$\begin{displaymath} \sum_{k=1}^nk^2{n\choose k}=n\cdot 2^{n-1}+n(n-1)2^{n-2}.\end{displaymath}$

12. Osoita, että

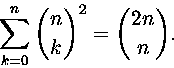
$\begin{displaymath} \sum_{k=0}^n{n\choose k}^2={2n\choose n}.\end{displaymath}$

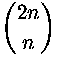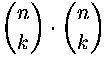Kohdan 11 nojalla $\displaystyle{2n\choose n}$ on origosta koordinaattipisteeseen $(n,\,n)$ johtavien reittien lukumäärä. Origosta pisteeseen $(n-k,\,k)$ on saman numeron mukaan $\displaystyle{n\choose k}$ reittiä. Mutta symmetrian nojalla pisteestä $(n-k,\,k)$ pisteeseen $(n,\,n)$ on yhtä monta reittiä. Pisteen $(n-k,\,k)$ kautta origosta pisteeseen $(n,\,n)$ kulkevia reittejä on niin ollen $\displaystyle{n\choose k}\cdot {n\choose k}$ kappaletta. Koska jokainen reitti origosta $(n,\,n)$ :ään kulkee tasan yhden pisteistä $(n-k,\,k)$ ,k=0, 1, ..., n kautta, on tehtävän kaava tosi. (Sama kaava saadaan kohteen 13 kaavasta (8), kun siinä asetetaan k=j=n.)

16. Miten alkaisivat funktioiden (1+x)^2/3 ja (1+x)^-2 x:n potenssien mukaan etenevät kehitelmät?

Jos $(1+x)^{2\over 3}=A+Bx+Cx^2+Dx^3+\cdots$ , niin

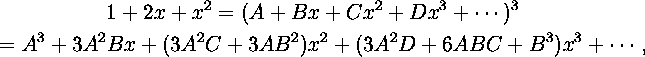
$\begin{gather*} 1+2x+x^2=(A+Bx+Cx^2+Dx^3+\cdots)^3\\ = A^3+3A^2Bx+(3A^2C+3AB^2)x^2+(3A^2D+6ABC+B^3 )x^3+\cdots,\end{gather*}$
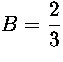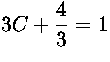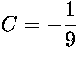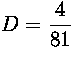joten A=1, $B=\displaystyle{2\over 3}$ , $3C+\displaystyle{4\over 3}=1$ eli $C=-\displaystyle{1\over 9}$ , 3D=-6ABC- B³ eli $D=\displaystyle{4\over 81}$ jne. Geometrisen sarjan summan kaavan perusteella $(1+x)^{-1}=1-x+x^2-x^3+\cdots$ . Siis $(1+x)^{-2}=(1-x+x^2- x^3+\cdots)^2=1-2x+3x^2-4x^3+\cdots$ .

Matti Lehtinen

[email protected]

Solmu 2/1996-1997