![[kaava]](/1997/1/retki10.gif)
Retki tehtiin Solmussa 2. Nyt on vielä tehtävä
eli tuolloin selityksettä tai ratkaisutta jääneiden kohtien tai tehtävien selittäminen.
Osoita, että kaikilla luonnollisilla luvuilla n ja kaikilla reaaliluvuilla x > -1 pätee
![[kaava]](/1997/1/retki10.gif)
Aloitetaan induktio arvosta n = 0. Selvästikin
1 + 0·x = 1 = (1 + x)0.
Oletetaan sitten, että 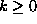 ja että
ja että 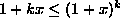 . Koska
. Koska
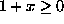 ja
ja
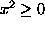 , on myös
, on myös
![[kaava]](kaava50.gif)
Induktioaskel on otettu ja väite todistettu.
Osoita, että
![[kaava]](/1997/1/retki21.gif)
Vihjeen mukaan osoitetaan ensin, että
![[kaava]](kaava51.gif)
Olkoon 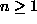 ja
ja
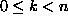 . Silloin todellakin
. Silloin todellakin
![[kaava]](kaava52.gif)
Binomikaavan induktiotodistuksen aluksi havaitaan, että
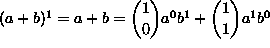 .
Otetaan
sitten induktioaskel, jonka pohjaksi oletetaan, että
.
Otetaan
sitten induktioaskel, jonka pohjaksi oletetaan, että 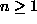 ja
että
ja
että
![[kaava]](kaava53.gif)
Silloin
![[kaava]](kaava54.gif)
Tasoon piirretään n suoraa; näistä mitkään kaksi eivät ole yhdensuuntaisia eivätkä mitkään kolme leikkaa toisiaan samassa pisteessä. Moneenko osaan suorat jakavat tason?
Merkitään n:n suoran synnyttämien jako-osien määrää f(n):llä. Jos suoria on n + 1, ja näistä yksi, suora l, poistetaan, jako-osia on siis f(n) kappaletta. Suora l leikkaa n muuta suoraa, ja se kulkee n + 1:n jako-osan läpi jakaen kunkin näistä kahteen osaan. (Tämä perustuu siihen, että jako-osat ovat kuperia monikulmioita; syntyvät uudet jako-osat ovat edelleen tällaisia.) Siten f(n + 1) = f(n) + n + 1. Väitetään, että f(n) = n(n + 1)/2 + 1. Tämä on totta, kun n = 0 (f(0) = 1). Jos f(n) = n(n+1)/2 + 1, niin f(n + 1) = f(n) + n + 1 = n(n + 1)/2 + n + 2 = (n + 1)(n/2 + 1) + 1 = (n + 1)(n + 2)/2 + 1.
Todista: jokainen kokonaisluku n>1 on joko alkuluku tai alkulukujen tulo.
Todistus. Kokonaisluku 2 on alkuluku. Oletetaan, että jokainen
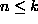 on joko alkuluku tai alkulukujen tulo.
Luku k + 1 on joko
alkuluku tai yhdistetty luku. Jos se on yhdistetty luku, se on
tulo k = ab, missä a ja b ovat
on joko alkuluku tai alkulukujen tulo.
Luku k + 1 on joko
alkuluku tai yhdistetty luku. Jos se on yhdistetty luku, se on
tulo k = ab, missä a ja b ovat 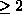 ja siis
ja siis 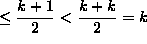 .
Induktio-oletuksen mukaan a ja
b ovat alkulukuja tai alkulukujen tuloja. Siis k + 1 on alkuluku
tai alkulukujen tulo.
.
Induktio-oletuksen mukaan a ja
b ovat alkulukuja tai alkulukujen tuloja. Siis k + 1 on alkuluku
tai alkulukujen tulo.
Olkoon n > 1 ja M positiivinen kokonaisluku.
Todista, että on olemassa yksikäsitteisesti määrätyt
kokonaisluvut
![[kaava]](/1997/1/retki41.gif) ja a0, a1, ..., am
siten, että am > 0,
ja a0, a1, ..., am
siten, että am > 0,
![[kaava]](/1997/1/retki44.gif) , kun
j=0, 1, ..., m, ja
, kun
j=0, 1, ..., m, ja
M = amnm + am-1nm-1 + ... + a0.
On olemassa m = m(M) siten, että 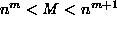 .
Suoritetaan induktio m:n suhteen. Jos m = 0, voidaan
valita a0 = M, ja väite pätee. Oletetaan, että väite pätee
kaikille M, joille
.
Suoritetaan induktio m:n suhteen. Jos m = 0, voidaan
valita a0 = M, ja väite pätee. Oletetaan, että väite pätee
kaikille M, joille
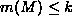 . Olkoon sitten M luku, jolle
m(M) = k + 1. Siis
. Olkoon sitten M luku, jolle
m(M) = k + 1. Siis 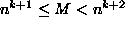 .
Olkoon vielä p < n
suurin kokonaisluku, jolla
.
Olkoon vielä p < n
suurin kokonaisluku, jolla 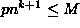 .
Silloin joko M = pnk+1 tai
0 < M - pnk+1 < nk+1. Edellisessä tapauksessa M:llä on
vaaditunlainen esitys, ja jälkimmäisessä tapauksessa
.
Silloin joko M = pnk+1 tai
0 < M - pnk+1 < nk+1. Edellisessä tapauksessa M:llä on
vaaditunlainen esitys, ja jälkimmäisessä tapauksessa
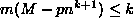 ,
joten M - pnk+1:llä on haluttua muotoa
oleva esitys n:n korkeintaan astetta k olevana polynomina. Kun
valitaan ak+1 = p, saadaan M:lle esitys n:n astetta k + 1
olevana polynomina.
,
joten M - pnk+1:llä on haluttua muotoa
oleva esitys n:n korkeintaan astetta k olevana polynomina. Kun
valitaan ak+1 = p, saadaan M:lle esitys n:n astetta k + 1
olevana polynomina.
Määritä x2:n kerroin polynomissa (1 + x + x2 + ... + xn)n.
Olkoon (1 + x + x2 + ... + xn)n
= 1 + anx + bnx2 + ... + xn2,
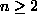 . Silloin
. Silloin
![[kaava]](kaava86.gif)
Siis an+1 = an + 1 ja bn+1 = an + bn + 1. Koska (1 + x + x2)2=1 + x2 + x4 + 2x + 2x2 + 2x3, a2 = 2 ja b2 = 3. Tästä seuraa, että an = n ja bn+1 = bn + n + 1 eli bn on n:n ensimmäisen positiivisen kokonaisluvun summa, siis bn = n(n + 1)/2.
Montako kaksialkioista osajoukkoa on n-alkioisella joukolla?
Olkoon kysytty lukumäärä f(n). Silloin f(1) = 0 ja f(2) = 1. Joukolla {a1, a2, ..., an, b} on f(n) kaksialkioista osajoukkoa {ai, aj} ja n kaksialkioista osajoukkoa {ai, b}. Siis f(n + 1) = f(n) + n. Väitetään, että f(n) = n(n - 1)/2. Tämä on totta, kun n = 1 ja n = 2. Jos f(k) = k(k - 1)/2, niin f(k + 1) = k(k - 1)/2 + k = k(k + 1)/2, niin kuin pitääkin.
Montako lävistäjää on kuperalla n-kulmiolla?
Monikulmion kärkiä yhdistäviä janoja on yhtä monta kuin n-alkioisella joukolla on 2-alkioisia osajoukkoja, eli edellisen mukaan n(n - 1)/2 kappaletta. Näistä janoista n kappaletta, monikulmion sivut siis, ei ole lävistäjiä, joten lävistäjiä on n(n - 1)/2 - n = n(n - 3)/2 kappaletta.
Monellako eri tavalla n lukua voidaan kirjoittaa jonoon?
Todistetaan induktiolla, että kysytty lukumäärä on n! = 1·2···n. Näin on varmasti, kun n = 1. Oletamme, että k lukua a1, a2, ..., ak voidaan kirjoittaa jonoon k! eri tavalla. Jokainen näistä järjestyksistä tuottaa k + 1 eri järjestystä luvuille a1, a2, ..., ak+1, koska ak+1 voidaan sijoittaa jo olemassa olevaan k:n luvun jonoon ensimmäiseksi tai minkä hyvänsä luvun aj, j = 1, 2, ..., k, jälkeen.
Olkoon f(n) luku, joka ilmoittaa, kuinka monella eri tavalla n lukua a1, a2, ..., an voidaan kirjoittaa jonoon niin, että jonon k:s luku on aina eri kuin ak, k = 1, 2, ..., n. Osoita, että f(n + 1) = n(f(n) + f(n - 1)).
Luvut a1, a2, ..., an ja an+1 voidaan sekoittaa tehtävässä ilmoitetuin ehdoin kahdella eri menetelmällä. Voidaan sekoittaa ensin n ensimmäistä lukua niin, että k:s luku on aina eri kuin ak, ja vaihtaa sitten an+1 ja jokin ak. Tällaisia sekoituksia on yhteensä nf(n) kappaletta; an+1 ei koskaan ole k:s luku. Toinen tapa on vaihtaa ensin ak ja an+1 ja sekoittaa sitten loput n - 1 lukua. Tällaisia sekoituksia on kaikkiaan nf(n - 1) kappaletta. Kaikki mahdolliset sekoitukset on tässä tullut otetuksi huomioon, sillä joka tapauksessa n + 1:lle paikalle tulee joko se luku, jonka an+1 korvaa (jälkimmäinen tapaus) tai jokin muu luku (edellinen tapaus). Siis f(n + 1) = n(f(n) + f(n - 1)).
Todista: 2!·4!···(2n)! > ((n + 1)!)n - 1.
Koska 2! = (1 + 1)!1, induktio pääsee alkuun. Oletetaan, että 2!·4!···(2k)!>((k + 1)!)n - 1. Silloin 2!·4!···(2k)!·(2(k + 1))! + 1 > ((k+1)!)k(2k+2)! = ((k + 1)!)k+1·(k + 2)(k + 3)···(2k + 2) > ((k + 1)!)k+1(k+2)k+1 = ((k+2)!)k+1.
Osoita: jos n on positiivinen kokonaisluku, niin f(n) = (n5)/5 + (n4)/2 + (n3)/3 - n/30 on kokonaisluku.
Selvästi f(0) = 0 ja f(1) = 1. Oletetaan, että f(k) on kokonaisluku. Silloin f(k + 1) = (k + 1)5/5 + (k + 1)4/2 + (k + 1)3/3 - (k + 1)/30 = f(k) + f(1) + (5k4 + 10k3 + 10k2 + 5k)/5 + (4k3 + 6k2 + 4k)/2 + (3k2 + 3k)/3; siis f(k + 1) on kokonaisluku.
Olkoon ![[kaava]](/1997/1/retki60.gif) . Osoita, että
. Osoita, että
![[kaava
]](/1997/1/retki61.gif)
Selvästi sin x>0 ja 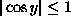 kaikilla y. Tehtävän väite
on tosi, kun n = 1. Oletetaan, että
kaikilla y. Tehtävän väite
on tosi, kun n = 1. Oletetaan, että
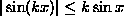 . Silloin
. Silloin
![[kaava]](kaava55.gif)
Kolmen pylvään A, B ja C ympärille voidaan pinota erikokoisia renkaita. Alkuasetelmassa pylväässä A on n rengasta, suuruusjärjestyksessä pienin päällimmäisenä, ja ne on siirrettävä torniin C samaan järjestykseen. Vain yhtä rengasta kerrallaan saa siirtää, eikä missään pylväässä saa koskaan olla pienempi rengas suuremman alla. Montako siirtoa vähintään tarvitaan?
Merkitään renkaiden siirtämiseen tarvittavien siirtojen
vähimmäismäärää f(n):llä. Silloin f(1) = 1. Koska
alinta rengasta ei voi liikuttaa, ennen kuin kaikki sen päällä
olevat n - 1 rengasta on siirretty, alin rengas voidaan
siirtää paikalleen pylvääseen C aikaisintaan silloin, kun
muut renkaat on siirretty pylvääseen B. Tähän tarvitaan
vähintään f(n - 1) siirtoa. Jotta muut renkaat tämän
jälkeen saataisiin siirretyiksi pylvääseen C, tarvitaan
taas ainakin f(n - 1) siirtoa. Siis
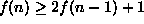 .
Kuvattu menetelmä mahdollistaa siirtojen tekemisen niin,
että f(n) = 2f(n - 1) + 1. Osoitetaan vielä, että f(n) =
2n - 1. Kaava on tosi, kun n = 1.
Oletetaan, että f(n - 1) = 2n-1 - 1. Silloin
f(n) = 2f(n - 1) + 1 = 2n - 2 + 1 = 2n - 1.
.
Kuvattu menetelmä mahdollistaa siirtojen tekemisen niin,
että f(n) = 2f(n - 1) + 1. Osoitetaan vielä, että f(n) =
2n - 1. Kaava on tosi, kun n = 1.
Oletetaan, että f(n - 1) = 2n-1 - 1. Silloin
f(n) = 2f(n - 1) + 1 = 2n - 2 + 1 = 2n - 1.
Binomikertoimet liitetään tavallisesti ranskalaiseen Blaise Pascaliin (1623-62). "Pascalin kolmio"
| 1 | ||||||||||||
| 1 | 1 | |||||||||||
| 1 | 2 | 1 | ||||||||||
| 1 | 3 | 3 | 1 | |||||||||
| 1 | 4 | 6 | 4 | 1 | ||||||||
| 1 | 5 | 10 | 10 | 5 | 1 | |||||||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||||||
| . . . | ||||||||||||
oli tuttu jo keskiajan kiinalaisille samoin kuin muutamille Pascalin eurooppalaisille edeltäjille.
Binomikertoimien
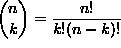 ,
,
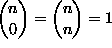 eli Pascalin kolmion
lukujen perusominaisuus on kolmiosta näkyvä yhteenlaskukaava
eli Pascalin kolmion
lukujen perusominaisuus on kolmiosta näkyvä yhteenlaskukaava
| (1) |
![[kaava]](kaava56.gif)
|
|---|
Lukujen 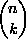 määritelmästä seuraavat heti
kaavat
määritelmästä seuraavat heti
kaavat
| (2) |
![[kaava]](kaava57.gif)
|
|---|
ja
| (3) |
![[kaava]](kaava58.gif)
|
|---|
Induktiolla on helppo todistaa (ks. Retki 1) oikeaksi binomikaava
| (4) |
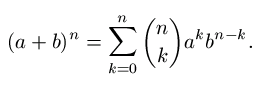
|
|---|
Binomikertoimien merkitys todennäköisyyslaskennassa ja
kombinaatio-opissa perustuu siihen, että sellaisella joukolla,
jolla on tasan n alkiota, on 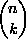 kappaletta k-alkioisia osajoukkoja. Tätä lukumäärää oli
aikaisemmin tapana kutsua n:n alkion k:ttain
otettujen kombinaatioiden lukumääräksi. - Joskus on
tarkoituksenmukaista määritellä, että
kappaletta k-alkioisia osajoukkoja. Tätä lukumäärää oli
aikaisemmin tapana kutsua n:n alkion k:ttain
otettujen kombinaatioiden lukumääräksi. - Joskus on
tarkoituksenmukaista määritellä, että
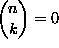 , kun k < 0 tai n < k.
, kun k < 0 tai n < k.
Todista oikeiksi yhteenlaskukaavat
![[kaava]](kaava87.gif)
Nämä yhteenlaskukaavat luovat näppärän keinon laskea peräkkäisten
kokonaislukujen potenssien summia. Yksinkertaisin tapaus perustuu havaintoon
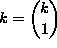 .
Tämän nojalla
.
Tämän nojalla
![[kaava]](kaava60.gif)
Laskeaksemme summan 12+22+...+n2 huomaamme ensin, että kun
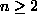 , niin
, niin
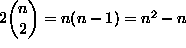 . Niinpä
. Niinpä
![[kaava]](kaava61.gif)
Laske
![[kaava]](kaava62.gif)
Tällaisten summien laskeminen oli tärkeää integraalilaskennan
syntyvaiheiden aikaan 1600-luvulla. Käyrän y = xp,
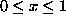 , kuvaajan alle jäävä pinta-ala eli
, kuvaajan alle jäävä pinta-ala eli
![[kaava]](kaava63.gif)
on suurilla n:n arvoilla suunnilleen sama kuin
![[kaava]](kaava64.gif)
Määritä edellisten tulosten perusteella
![[kaava]](kaava65.gif)
Binomikaavan perusteella on selvää, että
![[kaava]](kaava66.gif)
Samalla periaatteella saadaan monia muitakin kaavoja, kuten esimerkiksi
![[kaava]](kaava67.gif)
Kaavan (2) avulla voidaan laskea
| (5) |
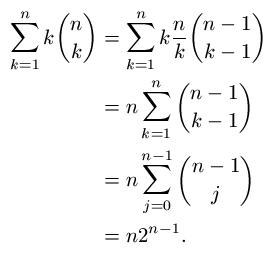
|
|---|
Vastaavalla tavalla saadaan
| (6) |
![[kaava]](kaava69.gif)
|
|---|
Kaavojen (5) ja (6) tapaiset kaavat voidaan johtaa aivan toisenlaisella menetelmällä, käyttämällä binomikaavaa ja differentiaali- ja integraalilaskentaa. Derivoidaan kaava
![[kaava]](kaava70.gif)
jolloin saadaan
![[kaava]](kaava71.gif)
asetetaan x = 1, ja on saatu kaava (5).
Johda kaava (6) integroimalla binomikaava.
Määritä
![[kaava]](kaava72.gif)
Eräs merkitys binomikertoimille 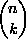 samoin kuin koko joukko niiden ominaisuuksia voidaan johtaa
seuraavan havainnon nojalla. Tarkastellaan tason niitä
koordinaattipisteitä, joiden koordinaatit ovat ei-negatiivisia
kokonaislukuja (ruutupaperi on hyvä malli), ja pisteestä
(0,0) alkavia reittejä, jotka koostuvat vain muotoa
(p,q) -> (p+1,q) ja (p,q) -> (p,q+1) olevista
askeleista. Pisteeseen (n,k) päättyvien eri reittien
lukumäärä on
samoin kuin koko joukko niiden ominaisuuksia voidaan johtaa
seuraavan havainnon nojalla. Tarkastellaan tason niitä
koordinaattipisteitä, joiden koordinaatit ovat ei-negatiivisia
kokonaislukuja (ruutupaperi on hyvä malli), ja pisteestä
(0,0) alkavia reittejä, jotka koostuvat vain muotoa
(p,q) -> (p+1,q) ja (p,q) -> (p,q+1) olevista
askeleista. Pisteeseen (n,k) päättyvien eri reittien
lukumäärä on 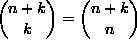 .
Että näin on, voidaan todistaa
induktiolla luvun n + k suhteen. Väite on varmasti tosi, kun
n + k = 1: selvästikin on vain
.
Että näin on, voidaan todistaa
induktiolla luvun n + k suhteen. Väite on varmasti tosi, kun
n + k = 1: selvästikin on vain  reittiä
pisteisiin (1,0) ja (0,1). Oletetaan sitten, että kaava
pitää paikkansa arvolla n + k - 1 ja jaetaan pisteeseen (n,k)
johtavat reitit kahteen luokkaan, pisteen (n-1,k) kautta
kulkeviin ja pisteen (n,k-1) kautta kulkeviin. Jos n =
0 tai k = 0, niin toinen näistä luokista on tyhjä; muissa
tapauksissa näissä luokissa olevien reittien määrä on
induktio-oletuksen nojalla
reittiä
pisteisiin (1,0) ja (0,1). Oletetaan sitten, että kaava
pitää paikkansa arvolla n + k - 1 ja jaetaan pisteeseen (n,k)
johtavat reitit kahteen luokkaan, pisteen (n-1,k) kautta
kulkeviin ja pisteen (n,k-1) kautta kulkeviin. Jos n =
0 tai k = 0, niin toinen näistä luokista on tyhjä; muissa
tapauksissa näissä luokissa olevien reittien määrä on
induktio-oletuksen nojalla 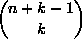 ja
ja
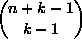 . Todistuksen viimeistelee
peruskaava (1).
. Todistuksen viimeistelee
peruskaava (1).
Osoita, että
![[kaava]](kaava73.gif)
Toinen menetelmä binomikertoimia koskevien kaavojen löytämiseksi
on osajoukkojen lukumäärän laskeminen. Oletetaan, että A
on joukko, jossa on n + k alkiota. Olkoon vielä
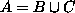 ,
missä B on n-alkioinen ja C
k-alkioinen (niin että
,
missä B on n-alkioinen ja C
k-alkioinen (niin että 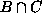 on tyhjä). Nyt jokainen
j-alkioinen
on tyhjä). Nyt jokainen
j-alkioinen 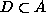 ,
(
,
(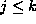 ) voidaan jakaa osiksi
) voidaan jakaa osiksi
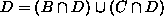 .
Osassa
.
Osassa 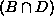 on, sanokaamme,
r alkiota ja osassa
on, sanokaamme,
r alkiota ja osassa 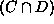 j - r alkiota. Toisaalta
jokainen yhdiste B:n r-alkioisesta osajoukosta ja
C:n j - r-alkioisesta osajoukosta on A:n
j-alkioinen osajoukko. Kun r saa kaikki arvot 0:sta j:hin,
tullaan tällä tavalla läpikäyneeksi kaikki A:n
j-alkioiset osajoukot. Osajoukkojen lukumääräksi tulee
j - r alkiota. Toisaalta
jokainen yhdiste B:n r-alkioisesta osajoukosta ja
C:n j - r-alkioisesta osajoukosta on A:n
j-alkioinen osajoukko. Kun r saa kaikki arvot 0:sta j:hin,
tullaan tällä tavalla läpikäyneeksi kaikki A:n
j-alkioiset osajoukot. Osajoukkojen lukumääräksi tulee
![[kaava]](kaava74.gif)
Toisaalta A:n j-alkioisten osajoukkojen määrä on
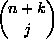 . Olemme saaneet kaavan
. Olemme saaneet kaavan
| (8) |
![[kaava]](kaava75.gif)
|
|---|
Binomikaavalla on paljon sovelluksia matemaattisessa analyysissä. Käytämme sitä nyt vakuuttautuaksemme "tunnetusta tosiseikasta", jonka mukaan aina kun a > 1 ja k on kiinteä positiivinen kokonaisluku, niin eksponenttifunktio an lopulta päihittää potenssifunktion nk. Asetetaan a = 1 + b, b > 0 ja valitaan n > 2k + 1 eli n - k > n/2. Verrataan nyt an:ää vain yhteen binomikaavan summan yhteenlaskettavaan:
![[kaava]](kaava76.gif)
Kun nyt valitaan vielä n suuremmaksi kuin (2k(k + 1)!)/(bk + 1), niin saadaan an>nk.
Mitä tapahtuu, jos eksponentti kaavassa (4) ei ole positiivinen kokonaisluku? Kokeillaan tapausta n = 1/2. Jotta olisi
![[kaava]](kaava77.gif)
olisi oltava
![[kaava]](kaava78.gif)
Yhtälö toteutuu varmasti, jos potenssien xk kertoimet ovat samat yhtälön molemmin puolin. Kokeillaan siis valintoja A2 = 1 eli (voidaan vielä valita) A = 1, 2AB = 1 eli B = 1/2, 0 = 2AC + B2 = 2C + 1/4 eli C = -1/8, 0 = AD + BC = D - 1/16 eli D = 1/16, 0 = 2AE + 2BD + C2 = 2E + 1/16 + 1/64 eli E = 5/128 jne.
Miten alkaisivat vastaavat kehitelmät funktioiden (1 + x)2/3 ja (1 + x)-2 tapauksissa?
Kaava (4) pitää muodollisesti paikkansa mille hyvänsä eksponentille:
![[kaava]](kaava79.gif)
Tietysti meidän tulisi varmistua, että yhtälön vasen puoli on kunnolla määritelty ja että oikealla puolella esiintyvän päättymättömän sarjan olemus tulee oikein ymmärrettyä. On mahdollista osoittaa, että kaava pätee, kun |x| < 1. Mutta se on jo toisen retken aihe.
***
Voitko johtaa kaavan (8) käyttämällä origosta lähtevien reittien lukumääriä?
Laske
![[kaava]](kaava80.gif)
Laske
![[kaava]](kaava81.gif)
Laske
![[kaava]](kaava82.gif)
Laske
![[kaava]](kaava83.gif)
Laske
![[kaava]](kaava84.gif)
Laske
![[kaava]](kaava85.gif)
Minkälainen olisi binomikaavan vastine tapauksessa (x + y + z)n?
Matti Lehtinen