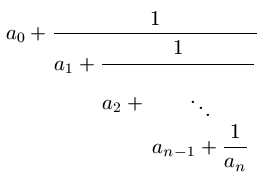
Äärellinen ketjumurtoluku on muotoa
| (1) |
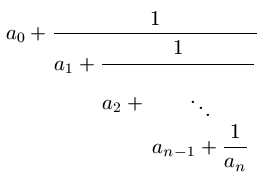
|
|---|
oleva lauseke, missä a0 on kokonaisluku ja a1, ..., an ovat positiivisia kokonaislukuja. Käytämme seuraavassa (1):lle myös hieman mukavampaa merkintätapaa [a0, ..., an]. On selvää, että äärellinen ketjumurtoluku (1) esittää rationaalilukua, jonka esitys muodossa p/q (p kokonaisluku ja q positiivinen kokonaisluku) saadaan lasketuksi (1):stä "alhaalta ylöspäin". Jos ketjumurtoluvussa on monta termiä, on sen arvon laskeminen tällä tavalla aika hankalaa. Tällöin voidaan käyttää seuraavia palautuskaavoja:
Olkoon p0 = a0, q0 = 1, p1 = a0 a1 + 1, q1 = a1 sekä
| (2) |
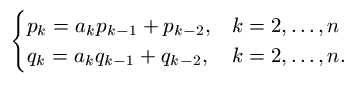
|
|---|
Voidaan osoittaa, että
| (3) |
![[a_0,...,a_k] = p_k/q_k, k=0,...,n](ketju-3.gif)
|
|---|
Esimerkki. Lasketaan x = [1,2,3,4,5] (3):n avulla. Nyt p0 = 1, p1 = 1·2 + 1 = 3, p2 = 3·3 + 1 = 10, p3 = 4·10 + 3 = 43, p4 = 5·43 + 10 = 225 ja samoin q0 = 1, q1 = 2, q2 = 3·2 + 1 = 7, q3 = 4·7 + 2 = 30, q4 = 5·30 + 7 = 157. Kaavan (3) mukaan on siis x = p4/q4=225/157. Lukija voi tarkistaa tuloksen kirjoittamalla ketjumurtoluvun [1,2,3,4,5] muotoon (1) ja laskemalla "alhaalta ylöspäin". Kannattaa myös laskea likiarvot luvuille pk/qk, k = 0, 1, ..., 4 ja verrata saatuja lukuja toisiinsa.
Tarkastellaan seuraavaksi käänteistä probleemaa: annettuna on rationaaliluku x=p/q (p kokonaisluku ja q positiivinen kokonaisluku) ja tehtävänä on esittää x äärellisenä ketjumurtolukuna (1). Sovelletaan lukuihin p ja q Eukleideen algoritmia, menetelmää, jota voidaan käyttää kahden luvun suurimman yhteisen tekijän määrittämiseen. Tämä menetelmä muodostuu perättäisistä jakolaskuista seuraavaan tapaan:
| p | = | a0q + r0, | 0 < r0 < q, |
| q | = | a1 q + r0 + r1, | 0 < r1 < q, |
| r0 | = | a2 r1 + r2, | 0 < r2 < r1, |
| ... | |||
| rn-3 | = | an-1 rn-2 + rn-1, | 0 < rn-1 < rn-2, |
| rn-2 | = | an rn-1 |
(jolloin lukujen p ja q s.y.t. on viimeinen nollasta eroava jakojäännös rn-1). Voidaan osoittaa, että x=p/q=[a0,a1,...,an].
Esimerkki. Tarkastellaan edellisen esimerkin lukua x=225/157. Eukleideen algoritmi antaa seuraavat jakolaskut
| 225 | = | 1·157 + 68, |
| 157 | = | 2·68 + 21, |
| 68 | = | 3·21 + 5, |
| 21 | = | 4·5 + 1, |
| 5 | = | 5·1 |
ja tulokseksi saamme ketjumurtoluvun [1,2,3,4,5], josta edellisessä esimerkissä juuri lähdimme liikkeelle.
Huomautamme lopuksi, että rationaaliluvun esitys äärellisenä ketjumurtolukuna ei ole yksikäsitteinen. Jos nimittäin esityksessä (1) viimeinen termi a_n > 1 (Eukleideen algoritmi antaa aina tällaisen esityksen) voidaan esitystä "jatkaa" korvaamalla an lausekkeella an - 1 + 1/1, toisin sanoen asettamalla uudeksi an:ksi vanha an - 1 ja uudeksi an+1:ksi luku 1. Esimerkiksi luvulla x = 225/157 on myös ketjumurtolukuesitys [1,2,3,4,4,1].
Tarkastellaan ääretöntä jonoa a0, a1,..., missä a0 on positiivinen kokonaisluku ja a1, a2,... ovat positiivisia kokonaislukuja. Tällöin jokaiselle ei-negatiiviselle positiiviluvulle n on xn = [a0, ..., an] määritelty äärellisenä ketjumurtolukuna. Lisäksi xn = pn/qn, missä pn ja qn saadaan palautuskaavoista (2). Voidaan osoittaa, että
| (5) |
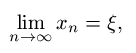
|
|---|
missä 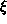 on
irrationaaliluku, toisin sanoen reaaliluku, joka ei ole
rationaaliluku. Sanomme nyt, että
on
irrationaaliluku, toisin sanoen reaaliluku, joka ei ole
rationaaliluku. Sanomme nyt, että 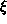 on äärettömän ketjumurtoluvun
[a0, a1, ...] arvo. Olkoon
on äärettömän ketjumurtoluvun
[a0, a1, ...] arvo. Olkoon 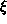 kääntäen mielivaltainen
irrationaaliluku. Voidaan kysyä, onko
kääntäen mielivaltainen
irrationaaliluku. Voidaan kysyä, onko 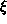 esitettävissä äärettömänä ketjumurtolukuna, toisin
sanoen onko olemassa ääretöntä jonoa
a0, a1, ..., jolle
esitettävissä äärettömänä ketjumurtolukuna, toisin
sanoen onko olemassa ääretöntä jonoa
a0, a1, ..., jolle 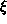 on ketjumurtoluvun
[a0, a1, ...] arvo. Vastaus
kysymykseen on myönteinen ja lisäksi voidaan osoittaa, että
esitys on yksikäsitteinen (toisin kuin äärellisten
ketjumurtolukujen tapauksessa). Näytämme seuraavassa, kuinka
kyseinen esitys löydetään. Olkoon
on ketjumurtoluvun
[a0, a1, ...] arvo. Vastaus
kysymykseen on myönteinen ja lisäksi voidaan osoittaa, että
esitys on yksikäsitteinen (toisin kuin äärellisten
ketjumurtolukujen tapauksessa). Näytämme seuraavassa, kuinka
kyseinen esitys löydetään. Olkoon
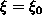 .
Olkoon
a0 suurin kokonaisluku, joka on enintään
.
Olkoon
a0 suurin kokonaisluku, joka on enintään
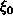 . Tällöin voidaan kirjoittaa
. Tällöin voidaan kirjoittaa
| (6) |
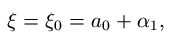
|
|---|
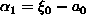 .
Tässä a0:n
määritelmän nojalla
.
Tässä a0:n
määritelmän nojalla
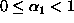 ja itse asiassa
ja itse asiassa
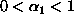 ,
koska
,
koska 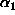 ,
joka on irrationaaliluku (jos
,
joka on irrationaaliluku (jos
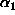 olisi rationaaliluku, olisi
olisi rationaaliluku, olisi
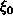 kahden
rationaaliluvun summana rationaalinen, mikä on ristiriita), ei
voi olla 0. Olkoon
kahden
rationaaliluvun summana rationaalinen, mikä on ristiriita), ei
voi olla 0. Olkoon
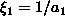 .
Tällöin
.
Tällöin 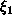 on
irrationaaliluku ja lisäksi
on
irrationaaliluku ja lisäksi
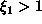 . Olkoon nyt
a1 suurin kokonaisluku, joka on enintään
. Olkoon nyt
a1 suurin kokonaisluku, joka on enintään
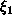 .
Tällöin a1 on positiivinen
kokonaisluku ja kuten edellä voidaan kirjoittaa
.
Tällöin a1 on positiivinen
kokonaisluku ja kuten edellä voidaan kirjoittaa
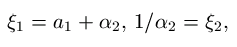
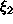 on irrationaaliluku ja
on irrationaaliluku ja
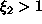 . Tällä tavalla
jatkaen saadaan ääretön jono
a0, a1, a2, ... ja voidaan
osoittaa, että äärettömän ketjumurtoluvun
[a0, a1, ...] arvo on
. Tällä tavalla
jatkaen saadaan ääretön jono
a0, a1, a2, ... ja voidaan
osoittaa, että äärettömän ketjumurtoluvun
[a0, a1, ...] arvo on
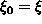 .
.
Huomattakoon, että aikaisemmin esittämämme Eukleideen
algoritmiin perustuva menetelmä rationaaliluvun äärelliseen
ketjumurtolukuesitykseen löytämiseksi on itse asiassa täsmälleen
sama kuin yllä oleva menetelmä sovellettuna rationaalilukuun
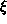 (menetelmää voidaan nimittäin
soveltaa niin kauan kuin luvut
(menetelmää voidaan nimittäin
soveltaa niin kauan kuin luvut 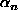 , jotka nyt olisivat rationaalisia, ovat nollasta
eroavia.)
, jotka nyt olisivat rationaalisia, ovat nollasta
eroavia.)
Ensimmäisenä esimerkkinä tarkastelemme
irrationaaliluvun 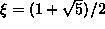 (kultaiseen leikkaukseen
liittyvä luku!) esitystä äärettömänä ketjumurtolukuna. Koska
(kultaiseen leikkaukseen
liittyvä luku!) esitystä äärettömänä ketjumurtolukuna. Koska
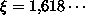 ,
on a0 = 1. Nyt
,
on a0 = 1. Nyt
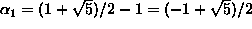 ,
joten
,
joten
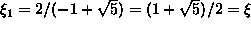 ja seurauksena on,
että
ja seurauksena on,
että
![ksii = [1, 1, 1, ...]](ksii=11.gif) .
Koska nyt an = 1,
n = 0,1,2,..., nähdään palautuskaavoista (2) nopeasti, että
tässä tapauksessa
pn/qn = Fn+2/Fn+1,
n=0,1,2,.... Tässä luvut Fn ovat tämän
lehden lukijoille tuttuja Fibonaccin lukuja (jotka
määritellään siten, että F1 = F2 = 1 ja
Fn+2 = Fn+1 + Fn).
.
Koska nyt an = 1,
n = 0,1,2,..., nähdään palautuskaavoista (2) nopeasti, että
tässä tapauksessa
pn/qn = Fn+2/Fn+1,
n=0,1,2,.... Tässä luvut Fn ovat tämän
lehden lukijoille tuttuja Fibonaccin lukuja (jotka
määritellään siten, että F1 = F2 = 1 ja
Fn+2 = Fn+1 + Fn).
Seuraavana esimerkkinä tarkastellaan luonnollisen logaritmijärjestelmän kantalukua, Neperin lukua e=2,71828···. Euler (1707-1783) todisti, että luku e voidaan esittää seuraavana äärettömänä ketjumurtolukuna
e = [2,1,2,1,1,4,1,1,6,1,1,8,1,1,...],
jossa siis kahta ykköstä seuraa parillinen luku, joka on kahta suurempi kuin edellinen parillinen luku.
Olkoon nyt 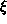 irrationaaliluku ja
[a0, a1, ...] siihen liittyvä
ketjumurtoluku. Rationaaliluvut
xn = pn/qn =
[a0, a1, ..., an],
ketjumurtoluvun [a0, a1, ...]
ns. konvergentit, lähenevät
irrationaaliluku ja
[a0, a1, ...] siihen liittyvä
ketjumurtoluku. Rationaaliluvut
xn = pn/qn =
[a0, a1, ..., an],
ketjumurtoluvun [a0, a1, ...]
ns. konvergentit, lähenevät 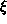 :tä siten, että ne
ovat vuorotellen pienempiä ja suurempia kuin
:tä siten, että ne
ovat vuorotellen pienempiä ja suurempia kuin 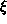 . Lisäksi ne
ovat parhaita approksimaatioita siinä mielessä, että
jos jollekin rationaaliluvulle x = r/s (r
kokonaisluku ja s positiivinen kokonaisluku) pätee
. Lisäksi ne
ovat parhaita approksimaatioita siinä mielessä, että
jos jollekin rationaaliluvulle x = r/s (r
kokonaisluku ja s positiivinen kokonaisluku) pätee
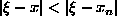 , niin tällöin
s > qn.
, niin tällöin
s > qn.
Esimerkki. Tarkastellaan tunnettua lukua
 = 3,14159... . Tämän irrationaaliluvun ääretön
ketjumurtolukuesitys alkaa siten, että a0 = 3,
a1 = 7, a2 = 15,
a3 = 1, a4 = 292. Toisin kuin
aikaisemmissa esimerkeissämme minkäänlaista säännönmukaisuutta
ei ole voitu tässä tapauksessa havaita. Tarkastellaan
konvergenttia
x3 = p3/q3 = 355/113
= 3,14159... . Tämän irrationaaliluvun ääretön
ketjumurtolukuesitys alkaa siten, että a0 = 3,
a1 = 7, a2 = 15,
a3 = 1, a4 = 292. Toisin kuin
aikaisemmissa esimerkeissämme minkäänlaista säännönmukaisuutta
ei ole voitu tässä tapauksessa havaita. Tarkastellaan
konvergenttia
x3 = p3/q3 = 355/113
 :n
likiarvona intialalisen matemaatikon Srinivasa Ramanujanin
(1887-1920) konstruoiman "ympyrän neliöimisen" valossa. Ympyrän
neliöimisessä on tarkoituksena konstruoida harpin ja
viivoittimen avulla neliö, jolla olisi sama ala kuin annetulla
ympyrällä. Jos ympyrän sädettä merkitään r:llä, olisi
siis konstruoitava jana (neliön sivu), jonka pituus on
:n
likiarvona intialalisen matemaatikon Srinivasa Ramanujanin
(1887-1920) konstruoiman "ympyrän neliöimisen" valossa. Ympyrän
neliöimisessä on tarkoituksena konstruoida harpin ja
viivoittimen avulla neliö, jolla olisi sama ala kuin annetulla
ympyrällä. Jos ympyrän sädettä merkitään r:llä, olisi
siis konstruoitava jana (neliön sivu), jonka pituus on
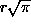 .
Voidaan kuitenkin osoittaa, että tämä on
mahdotonta suorittaa harpin ja viivoittimen avulla.
Tarkastellaan seuraavaa kuviota:
.
Voidaan kuitenkin osoittaa, että tämä on
mahdotonta suorittaa harpin ja viivoittimen avulla.
Tarkastellaan seuraavaa kuviota:
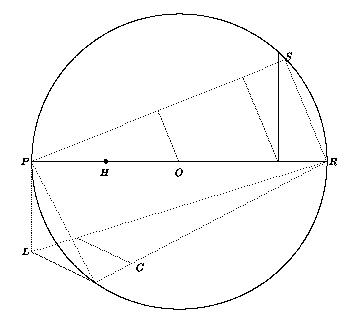
Kuvassa on piirrettynä annettu ympyrä, joka on tarkoitus "neliöidä". Sen keskipiste on O. Piste H on säteen PO keskipiste ja piste T säteellä OR sellainen, että jana TR on kolmasosa säteestä OR. Jana TQ on kohtisuorassa halkaisijaa PR vastaan ja jänne RS on piirretty yhtä pitkäksi kuin jana TQ. Yhdistetään pisteet P ja S ja piirretään janat OM ja TN yhdensuuntaisiksi janan RS kanssa. Piirretään jänne PK yhtä pitkäksi kuin PM ja piirretään tangentti PL=MN. Piirretään RL, RK ja KL. Piirretään RC yhtä pitkäksi kuin RH. Piirretään CD yhdensuuntaiseksi KL:n kanssa siten, että D sijaitsee janalla RL. Tällöin jana RD sivuna piirretyn neliön ala on melkein sama kuin ympyrän ala. Väite perustuu siihen, että kuten lukija voi helposti tarkistaa Pythagoraan lauseen ja yhdenmuotoisten kolmioiden avulla, janan RD pituus on yhtä kuin ympyrän säde kerrottuna luvun 355/113 neliöjuurella. Ramanujan antaa itse seuraavan esimerkin konstruktion tarkkuudesta: jos ympyrän ala on 140 000 neliömailia, niin konstruoitu jana RD eroaa "oikeasta" neliön sivusta noin yhden tuuman.
Tarkastelemme lopuksi jaksollisia ketjumurtolukuja. Sanomme, että ääretön ketjumurtoluku [a0, a1, ...] on jaksollinen, jos on olemassa sellainen ei-negatiivinen kokonaisluku k ja positiivinen kokonaisluku h, että
| ak+h+n = ak+n, | n=0,1,2,... |
Tämä tarkoittaa siis sitä, että jonossa a0, a1, ... alkiosta ak lähtien h peräkkäistä alkiota muodostavat jakson ak, ak+1, ..., ak+h-1, joka toistuu yhä uudelleen ja uudelleen. Merkitään jaksoa sen muodostamien alkioiden yli vedetyllä viivalla. Jaksollinen ketjumurtoluku on siis muotoa
![[a_0, a_1, ..., - a_k, ..., a_{k+h-1} -].](ketju-6b.gif)
![(1 + sqrt(5))/2 = [- 1 -]](152=1.gif) .
.
Sanomme, että irrationaaliluku 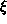 on kvadraattinen irrationaaliluku, jos se on
kokonaislukukertoimisen toisen asteen yhtälön juuri.
Esimerkiksi luku
on kvadraattinen irrationaaliluku, jos se on
kokonaislukukertoimisen toisen asteen yhtälön juuri.
Esimerkiksi luku 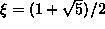 on kvadraattinen
irrationaaliluku, koska se toteuttaa yhtälön
on kvadraattinen
irrationaaliluku, koska se toteuttaa yhtälön
| (9) |
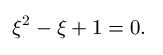
|
|---|
Ketjumurtolukujen teorian huomattavimpia tuloksia on seuraava lause, jonka Lagrange (1736-1813) todisti vuonna 1770.
Lause. Irrationaaliluvun 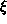 esitys äärettömänä ketjumurtolukuna
[a0, a1, ...] on jaksollinen silloin
ja vain silloin, kun
esitys äärettömänä ketjumurtolukuna
[a0, a1, ...] on jaksollinen silloin
ja vain silloin, kun 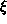 on
kvadraattinen irrationaaliluku.
on
kvadraattinen irrationaaliluku.
Yksinkertaisimpia kvadraattisia irrationaalilukuja ovat luvut
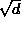 ,
missä d on positiivinen kokonaisluku,
joka ei ole neliö. Lagrangen lauseen mukaan näillä on
jaksolliset ketjumurtolukuesitykset. Tässä tapauksessa voidaan
vielä sanoa tarkemminkin, minkälainen esitys on muodoltaan.
Voidaan nimittäin todistaa, että esitys on muotoa
,
missä d on positiivinen kokonaisluku,
joka ei ole neliö. Lagrangen lauseen mukaan näillä on
jaksolliset ketjumurtolukuesitykset. Tässä tapauksessa voidaan
vielä sanoa tarkemminkin, minkälainen esitys on muodoltaan.
Voidaan nimittäin todistaa, että esitys on muotoa
![sqrt(d) = [a_0, - a_1, a_2, a_3, ..., a_3, a_2, a_1, 2a_0 -],](ketju-9a.gif)
missä jakson alkuosa on symmetrinen (tai puuttuu kokonaan.) Asiaa valaisemaan annettakoon muutamia esimerkkejä (joita lukija tietokoneen tai taskulaskimen avulla helposti voi hankkia lisää).
![sqrt(2) = [1, - 2 -] (symmetrinen osa puuttuu); sqrt(3) = [1, - 1, 2 -]](ketju-9b.gif)
Jukka Pihko